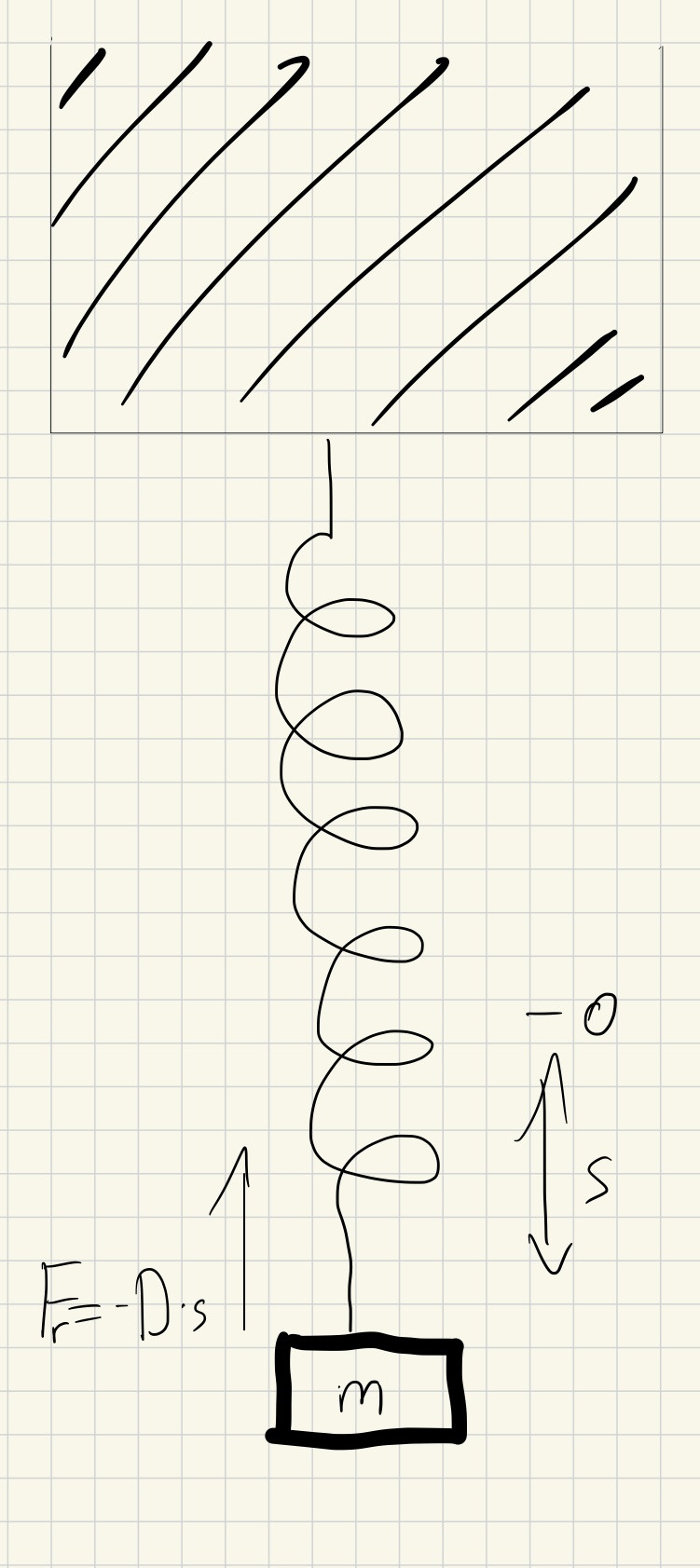1. Rücktreibende Kraft ist die Feder Kraft: \( F_{D}=F_{R} \rightarrow F_{R}=-D\cdot s \)
2. Alle wirkenden Kräfte mit der grundgleichung der mechanik gleichsetzen: \( F(t)=F_{R}(t) \rightarrow m \cdot \ddot{s} = -D \cdot s \)
3. Differentialgleichung aufstellen: \( \ddot{s}(t) = - \frac{D}{m} \cdot s(t) \)
4. Lösen der Differentialgleichung: was für s löst die Gleichung? Es gibt zwei Ansätze:

Exponentieller Ansatz:
\( y(t)= e^{at}, \dot{y}(t)= a \cdot e^{at}, \ddot{y}(t)=a^{2} \cdot e^{at} \)
In Funktion einsetzen:
\( a^{2} \cdot e^{at}=k \cdot e^{at} \) | \( :e^{at} \)
\( a^{2} = k \) | \( \sqrt{} \)
\( a = \sqrt{k} \), mit \( k= -\frac{D}{m} \)
\( a=\sqrt{- \frac{D}{m}} \)
Lösung: \( y(t)=e^{i \cdot \sqrt{ \frac{D}{m}} \cdot t} \) oder allgemein: \( y(t) = y_{0} \cdot e^{i\omega t - \phi_{0}} \)

Trigonometrischer Ansatz:
\( y(t) = \sin(at), \dot{y}(t) = a \cdot \cos(at), \ddot{y}(t) = - a^{2} \cdot \sin(at) \)
In Funktion einsetzen:
\( -a^{2} \cdot \sin(at) = k \cdot \sin(at) \) | \( :\sin(at) \)
\( -a^{2} = k \), mit \( k= -\frac{D}{m} \)
\( -a^{2} = -\frac{D}{m} \) | \( \sqrt{} \) | \( \cdot -1 \)
\( a = \sqrt{\frac{D}{m}} \)
Lösung: \( y(t) = \sin(\sqrt{\frac{D}{m}} \cdot t) \) oder allgemein: \( y(t) = y_{0} \cdot \sin(\omega t - \phi_{0}) \)
Damit ergibt sich für die Peiodendauer \( T=2 \pi \cdot \sqrt{\frac{m}{D}} \)